Monte-Carlo Tree Search, UCT, computer-Go and all that stuff

A revolution in planning originated in MCTS algorithms. Below an introduction and a survey (oriented to popularization).

Introduction (video / slides) in french: http://www-c.inria.fr/Internet/rendez-vous/modele-et-algo/prise-de-decision-sequentielle-dans-l-incertain-application-au-jeu-de-go

Slides in english: www.lri.fr/~teytaud/nicta.pdf


MCTS/UCT are algorithms for taking decisions in uncertain environments. The principles are:
- iteratively growing tree;
- random simulations.

Algorithmically, in the case of Go (you can generalize easily to other problems):

• a. First, you have in memory a tree with only one node, which is the current state of the Goban.
  
  

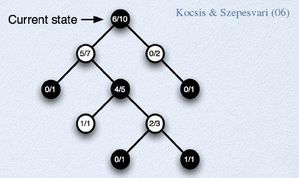
Example of UCT tree: each node "knows" its number of simulations and its number of wins. Thanks to David Silver, original author of this figure I guess.

• b. Then, start at the root, and find a path until a leaf; for each node, you choose the son which has highest exploration/exploitation value: the exploration/exploitation value is typically the sum of
  
  
  • the exploitation term: the percentage of won simulations from this son.
    
    
  • the exploration term: the square root of the ratio log(nb simulations of the parent) / (nb of simulations of this son)
  
  
  
• c. Then, randomly play from the leaf until the game is over.
  
  
• d. Then, update the statistics in the tree: update the number of simulations in each node, and the number of wins for black/white.
  
  
• e. If there is time left for thinking, go back to b.
  
  
• f. Play the most simulated move from the root.
  
  (this is UCT, the clearest version of MCTS; there are plenty of variations)
  
  
  
  
  
  
  1. Main tricks in MCTS / UCT
  
  MCTS and UCT refer to the same family of algorithms. The main initial publications are
  Kocsis et al (ECML 06), Coulom 06, Chaslot et al 06.
  
  A strong improvement in the Monte-Carlo part, showing in particular that the Monte-Carlo should not "only" play well but also keep diversity, is "fill board"; http://hal.inria.fr/inria-00117266
  
  There are several works around the parallelization; Cazenave, Chaslot et al,, Gelly et al http://hal.inria.fr/inria-00287867/en/.
  
  For the case of Go, but probably with more importance than just Go, the importance of preserving diversity has been emphasized in a post on the computer-Go mailing-list for the case of Nakade;

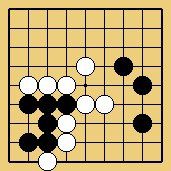
Example of Nakade, given by D. Feldmann.

a solution has been published in http://www.lri.fr/~teytaud/eg.pdf, and a more general diversity preservation mecanism (termed "fillboard") was also proposed with nice results in 19x19 Go (same paper).

Some Meta-level MCTS was proposed, with more or less good results; this was for example used for designing an opening book, better than no opening book at all, but less efficient than handcrafted opening books in spite of years of computational power.

Please notice that in spite of the optimism of an IEEE spectrum publication, classical techniques like alpha-beta did not succeed for the game of Go ("cracking go", 2007).

2. Links between MCTS and other existing algorithms

A* is a famous algorithm for e.g. shortest path. The idea consists in developing a tree of possible futures; the algorithm iteratively expands the non-expanded node with maximum "score", where the score is an estimate of the distance to the optimum.

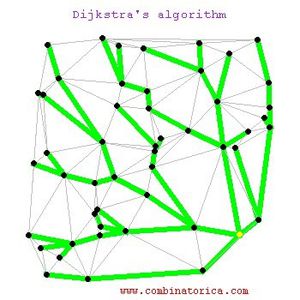
Dijkstra algorithm (related to A*), from combinatorica.com

The usual theoretical analysis of A* shows that it is "optimal" when the score is optimistic: it should (in a minimization problem) be a lower bound of the real value of the situation.

Optimism, a general view on MCTS/UCT, is exactly this. The interesting paper [Hren and Munos 08] http://www.springerlink.com/content/mu7227g225512347/ shows theoretical properties of "optimism" in the case of a proved bound.

UCT also iteratively expands the node with highest score. Usually, the score is computed also for already expanded nodes, but this is, I think, only for commodity of development.

Remark: A* has the notion of closed set, which is not used in usual MCTS implementations, whereas it makes sense. However, this is done in [De Mesmay et al 09] http://www.lri.fr/~rimmel/publi/TAG.pdf is an example in which there is an equivalent of "closed set".


3. Early publications related to MCTS/UCT

I like the reference Peret Garcia ECAI03, which was the first one in which I saw (out of games) the idea of locally developping a tree for the situation at which a decision should be taken. This idea might be considered as trivial for people working in games; it is not in areas in which the standart is Bellman's dynamic programming and variants.

I also like papers which try to have some learning from some branches to other branches, typically by evolutionary-like algorithms:
Fogel DB, Hays TJ, Hahn SL, and Quon J (2004) “A Self-Learning Evolutionary Chess Program,” Proceedings of the IEEE, Vol. 92:12, pp. 1947-1954.

An example of problem solved by the technique in Drake et al.

and Drake et al http://webdisk.lclark.edu/drake/publications/drake-gem2008-final.pdf

whenever for the moment these techniques do not work in the case of the game of Go.

The first ever win of a computer over a professional player in 19x19 (handicap 9, performed by MoGo against Kim Myungwan 8p in Portland 2008)

4. Results in computer-Go: computers vs humans

In 9x9 Go:
2007:win against a pro(5p)9x9(blitz) MoGo (Amsterdam)
2008:win against a pro(5p)9x9 MoGo (Paris)
2009:win against a pro(5p)9x9 as black MoGo (Rennes)
2009: win against a top pro (9p) 9x9 Fuego as white (Korea)

2009: win against a top pro (9p) 9x9 MoGoTW as black (Taipei)   (disadvantageous side!)

In 13x13 Go, MoGoTW won games against 6D players with H2 (2010) and MoGoTW won a game against a 5P player with handicap 2.5. (2011)

In 19x19 Go:
1998: ManyFaces looses with 29 stones against M. Mueller!
2008:win against a pro(8p)19x19,H9 MoGo (Portland)
2008:win against a pro(4p)19x19,H8 CrazyStone (Tokyo)
2008:win against a pro(4p)19x19,H7 CrazyStone (Tokyo)
2009:win against a pro(9p)19x19,H7 MoGo (Tainan), reproduced by Pachi in 2011 (IEEE SSCI)
2009:win against a pro(1p)19x19,H6 MoGo (Tainan)

Motoki Noguchi, the LLAIC organizers and a Go club of Clermont-Ferrand; mogo played 4 games against Motoki Noguchi (7D in France, professional level). MoGo won 2 games, but in one of them Motoki made a big mistake showing that he was perhaps not so concentrated at the end of the last game :-)

Comments

[cleaning company dubai]

One can find endless house cleaning topics to go over, from towels to environmental products…vacuums…how to unclutter and any list keeps growing. But a short time ago we happened upon interesting together with funny looking at cleaning your place!

[Intuit QuickBooks Support Number]

Get in touch Intuit QuickBooks Support USA, Canada by phone or email to learn more about our bookkeeping software solution or get quick help and support with your queries and clear your confusion. View our latest company news on QuickBooks Enterprises Phone Number and update your QuickBooks software through our tech. toll free number 1-888-867-9209

[IPhoen]

Heve u ever try to the find best christmas light house click me

[TTR]

Best Halloween Lighting Projector

[TTR]

Best Wine Bottle Lights for Christmas Decoration